Na letošní rok připadá 30. výročí pozorování fullerenů C60, C70 v plynné fázi, a pětadvacáté výročí jejich přípravy v krystalické formě (mimochodem i 40 let od prvého Czech-made příspěvku výzkumu nanouhlíků).
Po tak dlouhé době trochu překvapí, že třeba ve wikipedii (https://en.wikipedia.org/wiki/Fullerene_chemistry) přežívá obrázek s nesprávně umístěnými dvojnými vazbami:

Zdroj: Wikipedia, autor: Benjah-bmm27, licence obrázku public domain
Wikipedie v tom ovšem není zdaleka sama, jak ukazuje následujících pět dalších chybných obrázků, dokládajících, že žijeme v éře kavalírsky nonšalantní povrchnosti:
http://pubchem.ncbi.nlm.nih.gov/compound/Buckminsterfullerene#section=Top
http://www.sigmaaldrich.com/catalog/product/aldrich/572500?lang=en®ion=CZ
http://www.google.com/patents/WO2012005762A1?cl=en
http://www.chemspider.com/Chemical-Structure.110185.html
http://www.chem-station.com/chemist-db/archives/2011/11/-zen-ichi-yoshida.php
Když bylo dne 13. 9. 1990 zveřejněno NMR spektrum C60 (prvně na konferenci v nám blízké Kostnici), bylo to definitivním potvrzením hypotézy z r. 1985, že C60 má podobu jednoho ze třinácti (semi-regulárních) archimédovských mnohostěnů, jmenovitě komolého ikosaedru. Tato hypotéza sehrála svou roli v tom, komu připadla Nobelova cena za objev fullerenů, tedy trojici Robert Curl, Harold Kroto a Richard Smalley. Prakticky identický experiment totiž o rok dříve zveřejnila trojice Eric Rohlfing, Donald Cox a Andrew Kaldor z laboratoří Exxon, nepustila se však do hypotéz o struktuře C60. A Nobelova cena může mít nanejvýš tři laureáty. Nakonec i ten samotný článek s ikosaedrickou hypotézou z roku 1985 měl autorů pět, takže i zde muselo dojít na shortlisting (podobná situace dnes ale nastává často, nastala třeba i u vysvětlení oslabování ozonové vrstvy, nebo třeba i struktury DNA – Rosalind Franklinová zemřela před udělením ceny, zatímco Linus Pauling se s jejími výsledky nemohl včas seznámit, neb mu byl obstaven pas pro podezření z politicky nekorektních názorů). A to mezi těmi pěti ještě chyběla Číňanka Yuan Liu. Ta prováděla s H. Krotem úvodní experimenty, a byla nezbytná, neb Kroto přiletěvší z britského Sussexu ovládání aparatury ovšem neznal – leč Liu pak v polovině práce odjela na cesty.
Celá práce, která nakonec vedla k Nobelově ceně, byla hotova za nějakých 10 dnů (1.-11. 9. 1985), a oceněná trojice jinak nikdy před tím ani nikdy potom společně nepracovala. Poněkud kontroverzní zůstává ale i skutečnost, ze objevitelé efektivní syntézy fullerenů Donald Huffman a Wolfgang Krätschmer dosud ještě Nobelovu cenu nezískali, stejně jako objevitelé uhlíkových nanotrubiček. A nakonec, Nobelova cena za grafen také opomenula jeho prehistorickou přípravu už v roce 1962. C’est la vie. Anyhow – objev fullerenů BYL v mnoha ohledech jedinečnou událostí a je – nikoliv překvapivě – spojen s řadou neobvyklostí. Leč zpět k Archimedovi do třetího století před Kristem.
Řečený Archimedes je oním Archimedem, po němž je pojmenován základní hydrostatický zákon. Rozsah Archimedova díla však nelze dnes plně zmapovat v důsledku požáru knihovny s papyrovými svitky v egyptské Alexandrii. Není proto zcela jisté, že mu byl znám komolý ikosaedr, o kterém je zde řeč, ale z nepřímých evidencí se to předpokládá. Archimédovské mnohostěny jsou tvořeny dvěma či více pravidelnými mnohoúhelníky, přičemž jejich uspořádání kolem všech vrcholů je identické (a tedy NMR spektrum by bylo tvořeno jedinou linií). Jejich počet 13 byl znám nejpozději Keplerovi (při rozlišování chirálních struktur jich je 15).
Vedle to existují i regulární platónské mnohostěny, tvořené jen jedním typem pravidelných mnohoúhelníků. Těch je jen pět, mezi nimi ikosaedr tvořený dvaceti rovnostrannými trojúhelníky. Osekáním každého z jeho dvanácti vrcholů dostaneme komolý ikosaedr s vrcholy už šedesáti, což je geometrický předobraz C60. Je pokryt pravidelnými pětiúhelníky a šestiúhelníky. Univerzální vlastností vůbec všech fullerenů – nejen C60 – je, že vždy obsahují právě tucet pětiúhelníků. Ježto z každého vrcholu komolého ikosaedru vychází tři hrany, celkový počet vazeb v C60 (zatím nerozlišovaných na jednoduché a dvojné) je E=3*60/2=90. Dle Eulerovy formule pro vrcholy V, stěny F a hrany E konvexních mnohostěnů V + F – E = 2, je počet stěn F = 2 + 90 – 60 = 32, takže šestiúhelníků je 20.
Další důležitou geometrickou vlastností komolého ikosaedru je, že všechny jeho pětiúhelníky jsou tzv. izolované – každý je obklopen pěti šestiúhelníky (takže nikdy dva pětiúhelníky nesdílejí společnou vazbu). V C60 jsou jen dva typy vazeb: buď sdílené pěti- a šesti-úhelníkem (5/6 vazby), nebo dvěma šestiúhelníky (6/6 vazby). Vzhledem k právě tuctu pětiúhelníků je počet 5/6 vazeb 12 x 5 = 60, takže 6/6 vazeb je 90 – 60 = 30. V rámci geometrie je délka všech vazeb stejná, ne tak ale v C60. Např. výpočty provedené mezinárodním (japonsko-českým) týmem na Hokkaido univerzitě v období 1985-86 poskytly pro 5/6 vazby délku 1,464 Å, a pro 6/6 vazby 1,385 Å, což umožňuje formálně hovořit o jednoduchých a dvojných vazbách, a dosáhnout tak i formálně čtyřvazebného uhlíku.
Bez ohledu na to, zda 5/6 a 6/6 vazby mají stejnou nebo různou délku, patří geometrický komolý ikosaedr i C60 pod stejnou bodovou grupu symetrie – jmenovitě Ih. Před objevem fullerenů byla známy jen dvě chemické molekuly patřící pod tuto vysokou symetrii – uhlovodík dodekaedran C20H20 a dianioan [B12H12]2- (ikosaedrickou symetrii má ale i mnoho virů). Grupa symetrie kompaktně popisuje symetrické vlastnosti objektů – grupa Ih obsahuje zejména pěti- (procházejí středy protilehlých pětiúhelníků) a troj-četné osy symetrie (spojují středy protilehlých šestiúhelníků). Ty trojčetné osy souvisí s tím, že každý šestiúhelník je na přeskáčku obklopen třemi pěti- a třemi šesti-úhelníky. Ergo v každém šestiúhelníku jsou na přeskáčku tři jednoduché a tři dvojné vazby, což je zásadní rozdíl od benzenu, ve kterém je všech šest C-C vazeb identických (benzen patří pod D6h grupu symetrie, takže vykazuje šestičetnou osu, v C60 nepřítomnou). Na základě této geometrické rozvahy můžeme již zakreslit správné rozložení (formálních) dvojných vazeb v C60. Dvojné vazby jsou ty, které sdílejí dva šestiúhelníky, v každém jsou 3, celkem jich je 3 x 20 / 2 = 30. Eo ipso, musí to být takhle!
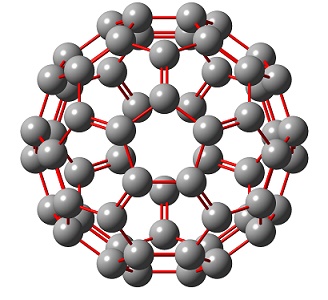
obrázek: (c) Zdeněk Slanina
Zdeněk Slanina
(o autorovi – Wikipedie)
obrázek u perexu: ilustrační, nejde o fulleren