Student World

S kužely a jehlany se setkáváme neustále, přičemž mohou mít různý tvar i velikost. Hromady písku, mušle přílipek, pyramidy, kostelní věže, vrcholy krystalů, rohy jednorožců a další objekty – všechny mají tento tvar. Každý kužel či jehlan má vrchol a základnu, která může být libovolným dvojrozměrným útvarem.
Představíme-li si vrchol jako maják se světelným zdrojem, pak bod leží v kuželu tehdy, padá-li jeho stín na základnu. Dokážeme, že pro objem kužele platí objem = 1/3 × obsah základny × výška.
Pohrajeme-li si trochu se stínováním (obrázek nahoře), vidíme, že pro všechny kužely i jehlany o stejné výšce a základnách se stejným obsahem mají řezy kteroukoli vodorovnou rovinou stejný obsah. Cavalieriho princip (předchozí kapitola)
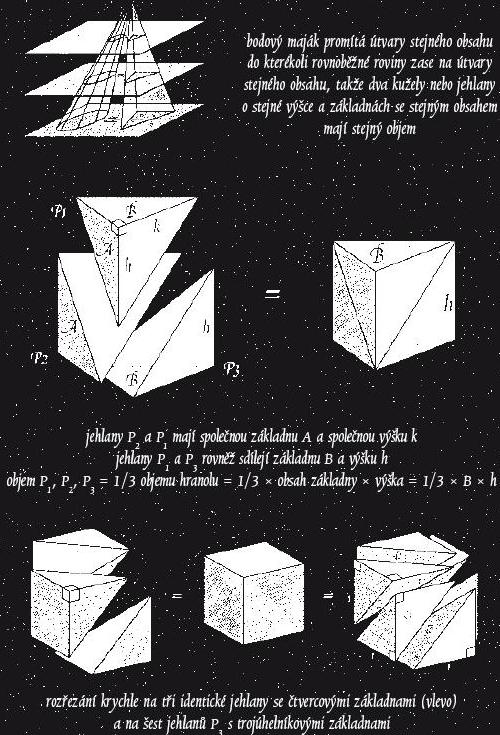
nám tedy říká, že všechna tato tělesa mají stejný objem. Stačí tudíž spočítat objem jednoho z nich, například pravoúhlého jehlanu (obrázek uprostřed). Tento jehlan spolu s dalšími dvěma jeho kopiemi je možné poskládat do kvádru s trojúhelníkovou základnou. Protože mají všechny tři jehlany stejný objem, má každý z nich objem rovnající se jedné třetině objemu tohoto kvádru. Q. E. D.
Při řezání krychle na šest jehlanů s trojúhelníkovými základnami ji nejprve rozřízneme diagonální rovinou na dva kvádry s trojúhelníkovými základnami a potom každý z nich na tři jehlany. Také ji lze rozříznout na tři stejné jehlany s čtvercovou základnou (obrázek dole) a pak každý z nich na jehlan P3 a jeho zrcadlový odraz. Vyrobíme-li si je všechny z papíru, získáme krásnou skládačku.

objem hromady písku = 1/3 Pi (r na 2) h objem jehlanu = 1/3 (a na 2) h

kuzely

bodový maják promítá útvary stejného obsahu do kterékoli rovnoběžné roviny zase na útvary stejného obsahu, takže dva kužely nebo jehlany o stejné výšce a základnách se stejným obsahem mají stejný objem

jehlany P2 a P1 mají společnou základnu A a společnou výšku k
jehlany P1 a P3 rovněž sdílejí základnu B a výšku h
objem P1, P2, P3 = 1/3 objemu hranolu = 1/3 × obsah základny × výška = 1/3 × B × h

rozřezání krychle na tři identické jehlany se čtvercovými základnami (vlevo) a na šest jehlanů P3 s trojúhelníkovými základnami

Tento text je úryvkem z knihy

Burkard Polster: Q. E. D. – Krása matematického důkazu
Dokořán 2014
O knize na stránkách vydavatele

autor