Student World

Se čtenářovým dovolením se zastavím u toho, jak jsem propadl tématu kolísání cen, oblasti, která pro mě byla mě něčím zcela novým. Tato fascinace pramenila už z mé dřívější práce na studiu hodně starého tématu – zákona distribuce osobních příjmů, který v 90. letech 19. století objevil Vilfredo Pareto (1848–1923). Má práce na tomto zákonu zaujala několik ekonomů a díky tomu jsem dostal pozvání promluvit na harvardském semináři, který řídil Hendrik S. Houthakker (1924–2008).

Když jsem vstoupil do „Hankovy“ kanceláře, zažil jsem překvapení, díky němuž se onen den stal jedním z nejpamátnějších v mém životě. Zvláštní diagram na jeho tabuli vypadal téměř stejně jako ten, který jsem chtěl načrtnout během své přednášky! Jak je možné, brzy jsem se ptal, že něco, co jsem právě objevil o příjmech, je už tady na tabuli? „Nemám tušení, o čem to mluvíte. Tenhle graf se týká cen bavlny.“ Než jsem přišel, pracoval s jedním studentem a tabuli ještě nestihl smazat.

Proč by měla souviset distribuce příjmů a bohatství ve společnosti s kolísáním cen bavlny? Proč by měly křivky obou dvou jevů mít stejný průběh se stejnými vydutími a vypouklinami? Mohlo by to odhalovat hlubší spojitost mezi oběma ekonomickými aspekty – snad jakési zvláštní skutečnosti, které se za těmito grafy skrývají? Teorie financí tehdy znovuobjevila jednu starou teorii, podle níž ceny kolísají způsobem, který odpovídá házení mincí. Hledali pro to důkazy, avšak spolehlivé doklady z historie nebylo lehké nalézt. Výjimkou byla právě bavlna.

Newyorská burza bavlny pečlivě udržuje záznamy každodenního pohybu cen za více než století, protože se tato důležitá surovina ve velkých množstvích přesunovala z amerického Jihu na průmyslový Sever. Téměř veškeré obchodování s bavlnou mezi americkými státy se soustřeďovalo na jedné burze. Pro ekonoma by to měla být vysněná fantazie, Houthakkerovi a jeho studentům to ale připadalo spíše jako noční můra. Ceny vykazovaly až příliš mnoho prudkých skoků vzhůru a hlubokých poklesů, přičemž míra kolísání se během doby neustále měnila. V některých letech byly ceny stabilní, v jiných zase divoce skákaly. „Dělali jsme všechno možné, abychom v tom našli nějaký smysl. Všechno se tam mění, nic není stálé. Je to chaos nejhoršího druhu.“ Nenašli způsob, jak na data aplikovat statistický model, vytvořený původně v roce 1900 – ten předpokládal, že změna ceny v daný den je nezávislá na změně z předešlého dne a její graf má mírně nepravidelný průběh, který lze předpovědět pomocí zvonové křivky.

Ihned jsme se dohodli: nechá mě, abych se podíval, co bych v tom mohl udělat. Podal mi kartonové krabice plné děrných štítků s daty. „Tak hodně štěstí. Pokud v tom něco najdete, dejte mi prosím vědět, co jste zjistil.“

Po návratu do IBM mi výpočetní středisko přidělilo programátora, aby ty záznamy analyzoval – stejným způsobem jako data o rozdělení příjmů. Kolik je v tom velkých cenových skoků, kolik malých? Kvůli své nízké pozici na firemním seznamu priorit jsem musel na výsledky dlouho čekat, tak jsem zajel vlakem na Manhattan, kde tehdy sídlil Národní úřad pro ekonomický výzkum. V jeho knihovně se nacházela řada prachem pokrytých knih plných tabulek s finančními statistikami – před érou počítačů to byl učiněný poklad. Později jsem ještě získal údaje z ministerstva zemědělství ve Washingtonu. Shromáždil jsem všechny dostupné statistiky a vybudoval si tak encyklopedii cen bavlny v jednotlivých dnech, týdnech, měsících a letech, celkem za více než 100 let.

To, co mi počítač pomohl najít, bylo pozoruhodné. Potvrdilo to Houthakkerův dojem: změny cen ze dne na den, z týdne, měsíce a roku na další týden, měsíc a rok se vůbec nechovaly tak, jak předpokládal model z roku 1900. Rozptyl dat se choval nepředvídatelně. Pokaždé, když jsem k datovému souboru přidal další cenovou změnu, můj odhad rozptylu se změnil a nikdy se neustálil, naopak nevyzpytatelně těkal sem a tam. Překvapovalo mě to, protože kvalita dat byla nezpochybnitelná. Navíc tam bylo příliš mnoho velkých cenových skoků, než aby se graf mohl vejít do Gaussovy zvonové křivky.

Dva modely cenových změn
Jak se mění ceny na organizovaných trzích zvaných burzy, kde se obchoduje s akciemi a komoditami?
Tyto trhy se celá staletí rozvíjely bez jakékoli podpory v podobě systematických matematických modelů. První z takových modelů předložil v roce 1900 francouzský matematik Louis Bachelier (1870–1946). Přišel podivuhodně brzy – daleko dříve, než k tomu dozrála doba – a byl opravdu zvláštní. Stal se z něj však standardní finanční model a právě ten se také Houthakker pokoušel aplikovat na ceny bavlny. Z finančního hlediska byl možná Bachelierův model vyspělý, nepodporovala ho ovšem vůbec žádná data. Ve své době větší pozornost nevyvolal, během času jej však vytáhly na světlo dvě události. Na teoretické frontě jej kolem roku 1920 znovuobjevil Norbert Wiener jako vhodný model významného fenoménu zvaného Brownův pohyb a toto zjištění se dál rozvíjelo ve 30. a 40. letech. Z praktického hlediska měl velký vliv nástup počítačů v 60. letech, který podpořil zkoumání dat i teorie.

Díky počítačům jsem mohl v předběžné zprávě z roku 1962 poukázat na chyby v Bachelierově modelu a předložit svou alternativní teorii, která se dala vyjádřit bez jediného vzorce, což nádherně zapadalo do mého divokého keplerovského snu. A v roce 1963 z toho vzešla má první studie na toto téma nazvaná „Kolísání určitých spekulativních cen“, která pak byla v ekonomické literatuře hojně citována. Teorie z roku 1900 předpokládala, že se (matematicky řečeno) „ceny mění spojitě“ a cenové skoky lze tedy zanedbat, a dále že se cenové změny řídí týmiž pravidly za prosperity i během krize. Teorie byla v rozporu s velkým množstvím dobře dokumentovaných dat a potřebovala tak časté a rozsáhlé úpravy. Má alternativní teorie z roku 1962 připouštěla nespojité změny a v letech 1965 a 1973 byla ještě rozšířena, aby zahrnovala střídající se období prosperity a krizí.

Všechny grafy cenového vývoje vypadají podobně. Jistě, některé směřují vzhůru, jiné dolů. Avšak v žádném měřítku – denním, měsíčním nebo ročním – mezi nimi žádný velký rozdíl není. Odstraníme-li konkrétní data a ceny, nejde poznat, který je který. Všechny jsou stejně „klikaté“. „Klikatost“ není příliš vědecký termín (a dokud jsem nevyvinul fraktální geometrii, neexistoval vhodný způsob, jímž by se dal tak vágní pojem kvantifikovat), nicméně je to přesně ona vlastnost, kterou v cenách bavlny vidíme nyní: fraktální vzor. Fraktální změny měřítka se zde neprovádějí s tvary kvítků v květenství nebo květáku, ale aplikují se na jinou strukturu, na kolísání cen. Samo jádro financí je fraktální. Kruh se tím uzavírá. Nebylo náhodou, že Houthakkerův graf cen bavlny vypadal stejně jako můj graf distribuce příjmů. Byla za nimi tatáž matematika.

Pečlivé testy, které vyvrátily Bachelierův model, v roce 1963 bohužel na nikoho nezapůsobily. Ekonomická věda usoudila, že moje práce je příliš komplikovaná a příliš cizí jejich oboru. Změny v oboru, které by představovala a které by se dále prohlubovaly, bylo těžké rozpracovat a prosadit. Zdálo se jim mnohem snazší pokračovat v nekonečné řadě oprav. Co jsem měl dělat? Přenesl jsem svoje priority na jiné obory a k cenovému kolísání jsem se vracel už jen sporadicky. Teorie z roku 1900, kterou jsem vyvrátil, žila dál a stále přitahovala řadu mladých matematiků a vědců, kteří svým odchodem oslabovali obory, z nichž odešli.
A pak, možná trochu později, než jsem čekal – až v roce 2008 – se na trzích stalo to, co se stát muselo: dostavil se krach.

Kepler versus Ptolemaios
Modely cenového kolísání, Bachelierův z roku 1900 a můj z roku 1963, byly prvními dvěma na tomto poli a hrály hlavní roli v událostech, které nastaly brzy poté. Je snad toto téma prokleté, že se už navždy bude popisovat z hlediska souboje obou modelů? Obávám se, že ano, a rád bych – se vší skromností – objasnil proč, na příkladu jedné klíčové události vědy: nahrazení chybného starověkého modelu pohybu planet Keplerovými elipsami. Ptolemaiův model tvrdil, že planety obíhají po kružnicích kolem Země, musel se ale opravovat pokaždé, když se pozorováním zjistily nějaké anomálie. Víra v něj se udržela až do počátku 17. století, kdy Kepler dokázal, že planety obíhají kolem Slunce po eliptických drahách.

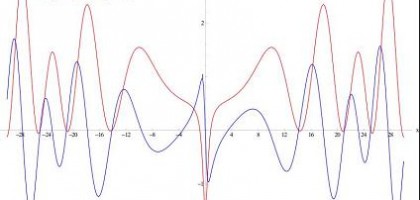
Bachelier předpokládal, že cenové změny sledují staré známé rozdělení četností zvané Gaussova křivka. Její klíčovou vlastností je, že velké odchylky od normy jsou velmi málo pravděpodobné, to znamená, že na nich nezáleží. Na následujících obrázcích cenových fluktuací představuje horní graf Bachelierův model, podle něhož je většina změn jenom drobnými odchylkami. Uprostřed máme graf reálného vývoje cen akcií IBM, v němž vidíme několik mimořádných odchylek a celkově mnohem větší kolísání než v Bachelierově modelu. Dolní graf vychází z mého počítačově generovaného multifraktálního modelu a je snad zřejmé, že mnohem lépe vystihuje skutečné změny cen na finančních trzích.

Obstaral jsem finančním datům racionální příbytek, nijak mě ale nepřekvapovalo, že o něm v té době zřejmě žádný člověk z praxe nevěděl. Za studia u Paula Lévyho jsem se seznámil s raritou, kterou on nazýval stabilita (a já ji pak nazval Lévyho stabilita). Díky ní lze identifikovat chování typické pro cenové změny. Naštěstí jsem v IBM měl přístup k počítači, na kterém se daly – byť velmi pracně – Lévyho stabilní hustoty poprvé skutečně vypočítat.

V případě bavlny můj model seděl zvláště nápadně – a bez švindlování. Má první práce v oboru financí propojila dvě oblasti, které k sobě měly velmi daleko. Stabilní rozdělení se kupodivu hodilo na každý detail datového souboru – zejména na symetrii jeho rozdělení, kterou počáteční výzkumy přehlédly.
Často se tvrdí, že pokud se sčítá velký počet statistických hodnot, je i ta největší z nich zanedbatelná ve srovnání s celkovým součtem. Dlouho už se ale ví, že to občas neplatí – avšak jen v případech, o něž se praktičtí statistikové nemusejí starat. Jeden hlučnější oponent opakovaně tvrdil, že tyto případy jsou „nepatřičné“, takový názor ho ale zavedl na scestí. Odborníci dokonce tyto případy dobře znali, dlouho je ale považovali jen za bezvýznamné záležitosti dobré leda tak pro čistou matematiku. Tím, že jsem je zatáhl do až příliš praktického oboru financí, vynikla nutnost ostře rozlišovat mezi „mírnými“ a „divokými“ stavy nahodilosti. Žádné minulé práce o cenách neměly ani tušení o nějaké „divokosti“ a sebejistě se opíraly o představu, že realitu řídí náhoda, která je „patřičná“, a tudíž mírná.

Tento text je úryvkem z knihy:
Benoit B. Mandelbrot: Fraktalista
Argo a Dokořán 2014
O knize na stránkách vydavatele

autor