Student World

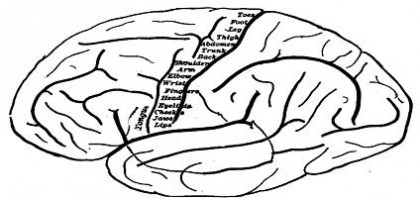
Schopnost rychle počítat nemá výraznou souvislost s porozuměním matematice nebo s tvořivostí. Jen nemnoho velkých matematiků zároveň umělo bleskově počítat a řada z nich byla dokonce v aritmetice dosti slabá. Alexandr Craig Aitken tuto schopnost měl a představoval výjimku, protože byl současně profesorem matematiky na Edinburské univerzitě. Aitken měl v roce 1954 přednášku pro londýnskou Inženýrskou společnost, kde vysvětlil některé ze svých metod, například algebraické zkratky, především ale mluvil o významu paměti. Aby své teze podpořil, vysypal ze sebe desetinný rozvoj zlomku 1/97, kde se číslice začínají opakovat až po 96 desetinných místech.

V závěru přednášky si povzdychl, že od chvíle, kdy si pořídil první kalkulačku, začaly jeho mentální schopnosti upadat. „Mentální počtáři jsou možná odsouzeni k vyhynutí, tak jako Tasmánci nebo Moriorové,“ předvídal. „Proto se můžete takovými jedinci zabývat podobně, jako se antropologové zajímají o výjimečný druh; někteří z mých dnešních posluchačů budou moci v roce 2000 říci: ,Ano, jednoho takového jsem znal.‘“
Tahle kalkulace však Aitkenovi nevyšla.

„Neurony! Připravit! Vpřed!“
S netrpělivým praskáním a šustěním obrátili listy svých testů účastníci násobícího kola Světového poháru v mentálním počítání. Soutěžní místnost na Lipské univerzitě utichla; 17 soutěžících se zamýšlelo nad první úlohou: 29 513 736 × 92 842 033.
Aritmetika je opět v módě. Třicet let poté, co první levné kalkulačky uspíšily úpadek schopnosti počítat „z hlavy“, přichází zpětný úder. V tisku denně nacházíte hlavolamy, cvičíte se pomocí populárních počítačových her s aritmetickými hádankami a na samé špici jsou bleskoví počtáři a jejich pravidelné mezinárodní turnaje. Světový pohár v mentálním počítání založil německý odborník na výpočetní techniku Ralf Laue v roce 2004; turnaj se koná každý druhý rok. Jde o spojení dvou Laueových životních koníčků: mentální aritmetiky a sbírání neobvyklých rekordů (jako je nejvyšší počet hroznů vržených během jedné minuty na vzdálenost 15 metrů a zachycených v ústech; těch je 55). Pomohl také internet, díky kterému nachází spřízněné duše (mentální aritmetici obecně nepatří mezi extroverty). Světové společenství lidských kalkulaček (matematických atletů neboli „matletů“) bylo silně zastoupeno právě v Lipsku, kde se sešli soutěžící z Peru, Íránu, Alžíru nebo Austrálie.

Jak se pozná výjimečná schopnost počítat? Laue převzal kategorie z Guinessovy knihy rekordů – násobení dvou osmimístných čísel, sčítání deseti desetimístných čísel, odmocniny šestimístných čísel (s přesností na osm desetinných čísel), vypočítání dne v týdnu pro jakékoli datum mezi lety 1600 a 2100. Poslední zmiňovaná metoda měří takzvaný kalendářní výpočet, což je ozvěna zlatého věku bleskového počítání, kdy se vystupující ptávali náhodné osoby z publika na jeho nebo její datum narození a okamžitě doplňovali odpovídající den v týdnu.
Podívaná ustoupila pravidlům a soutěživému duchu. Nejmladší soutěžící, jedenáctiletý Ind, předváděl „virtuální abakus“ – zuřivě mával rukama a přesouval imaginární kuličky, zatímco ostatní byli v klidu a potichu a jen občas zapisovali své odpovědi. (Podle pravidel smí soutěžící zapsat pouze závěrečnou odpověď.) Po uplynutí 8 minut a 25 sekund se s nadšením žáčka základní školy přihlásil Alberto Coto ze Španělska. V té chvíli totiž osmatřicetiletý soutěžící dokončil násobení dvou osmimístných čísel v rekordním čase. Byl to jistě úžasný výsledek, nicméně dívat se na něj bylo podobně strhující jako dohlížet na celou zkoušku.
V Lipsku nápadně chyběl nejslavnější matlet na světě, francouzský student Alexis Lemaire, který při měření počítacích schopností dává přednost jinému ukazateli. V roce 2007, když mu bylo 27 let, se dostal na první stránky novin poté, co za pouhých 70,2 sekundy v Londýnském muzeu přírodních věd spočítal třináctou odmocninu z čísla:
85 877 066 894 718 045 602 549 144 850 158 599 202 771 247 748 960 878 023 151 390 314 284 284 465 842 798 373 290 242 826 571 823 153 045 030 300 932 591 615 405 929 429 773 640 895 967 991 430 381 763 526 613 357 308 674 592 650 724 521 841 103 664 923 661 204 223.
Lemairův výkon byl zajisté více velkolepý. Číslo mělo 200 číslic a za 70,2 sekundy je lze sotva vyslovit. Ale znamená to, jak on sám tvrdí, že je nejlepší bleskový počtář všech dob? Mezi počtáři o tom panují veliké spory, které odráží bezmála dvě stě let starou bitvu mezi Zerahem Colburnem a Georgem Bidderem, z nichž každý byl výjimečný v určitém druhu počítání.
Pojem „třináctá odmocnina z a“ je číslo, které když vynásobíme třináctkrát jím samým, dostaneme a. Existuje pouze omezený počet čísel, která když se vynásobí třinácti, dosáhnou délky 200 číslic. (Jde o počet omezený, ale obrovský. Odpovědí může být jedno ze 400 bilionů čísel, všechna se skládají z 16 číslic a začínají dvojkou.) Protože 13 je prvočíslo a údajně má nosit smůlu, Lemairův výpočet měl jistou auru tajemna. Ve skutečnosti má třináctka řadu výhod. Například když dvojku třináctkrát znásobíme samu sebou, výsledné číslo končí dvojkou. Když trojku, výsledek končí číslem 3. Stejně je tomu s čísly 4, 5, 6, 7, 8 a 9. Jinými slovy poslední číslice třinácté odmocniny daného čísla je totožná s poslední číslicí původního. Tuto číslici dostaneme zdarma, bez nutnosti provádět výpočet.
Lemaire vypracoval algoritmy pro výpočet zbylých 14 číslic konečné odpovědi, ty ale nikomu neprozradil. Puristé tvrdí, nejspíš neoprávněně, že v jeho případě nejde ani tak o schopnost počítat, jako o memorování dlouhé řady čísel. Také poukazují na to, že Lemaire nemůže najít odmocninu jakéhokoli 200místného čísla, které mu zadáte. Tehdy v muzeu dostal na výběr z několika set čísel a mohl si vybrat jedno z nich.

Tento text je úryvkem z knihy
Alex Bellos: Alexova dobrodružství v zemi čísel
Dokořán 2015
O knize na stránkách vydavatele

autor